简单和多元线性回归的公式与从头实现

本身就是非常短的公式，做为ESL的第一课，非常基础。

有很多库可以做这件事，但正好我最近开发中需要用GPU计算回归（可以加速非常多倍），顺便写一篇博客来测试网站的公式显示是否正常。

什么是线性回归

简单地说就是用线性方程来表示数据的趋势。

一元： $y=mx+b$
多元： $y=m_1x_1+m_2x_2+...+b$

|1.5x
你可以考虑成每个点都是相同质量的恒星，回归线就是放一根长长的棍子，在这个重力环境下最后平衡的位置。

简单一元线性回归公式 (Linear regression)

Simple OLS regression 单独列出来是因为更直观和易于理解：

m=\frac {\sigma_{x, y}} {\sigma^2_x}=\frac {E[(X-\mu)(Y-\nu)]} { E[(X-\mu)^2] }

就是协方差除于x的方差，如何推导到此公式就省略不谈了，但你应该已经感受到了此公式的魅力。

然后b就是得出m后带入即可：

b=\bar{y} - m\bar{x}

pyTorch代码实现

用pyTorch是为了GPU加速。现在假设我们有一个y是2018-02月的NVDA价格数据：

import torch
y = torch.tensor([
    225.58, 228.8 , 217.52, 230.93, 228.03, 232.63, 241.42, 246.5 ,
    243.84, 249.08, 241.51, 242.15, 245.93, 246.58, 246.06, 242.  ,
    232.21, 236.54, 235.65, 242.16
])

然后我们生成x：

x = torch.arange(len(y)).float()

tensor([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12., 13.,
14., 15., 16., 17., 18., 19.])

回归代码（这里只为了可读性，有重复的计算）：

demean_x = x - x.mean()
demean_y = y - y.mean()
n_1 = x.shape[0] - 1
m = torch.sum(demean_x * demean_y / n_1) / torch.sum(demean_x ** 2 / n_1)
b = y.mean() - m * x.mean()
print(m, b)

(tensor(0.7734), tensor(230.4090))

让我们绘图看看效果：

from matplotlib import pyplot as plt
plt.plot(x, y)
plt.plot(x, m * x + b)
plt.show()

|1.5x
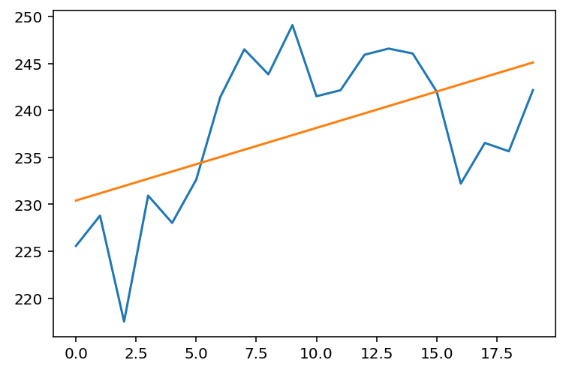
看起来不错🥂。

多元线性回归公式(Multiple Linear regression)

本质和简单回归一样，这里使用矩阵表达，且更是简短：

b,m_1,...,m_n=(X^TX)^{-1}X^Ty

一个公式都解决了，同样也适用于简单线性回归。

题外话， $X^TX$ 在各处都能见到，还有个私募名字就叫XTX。

pyTorch代码实现

公式内含了很多隐藏信息，而文字介绍又太繁琐，让我们用代码来实现下。

我一直觉得如果教科书和论文上的公式，都有相应代码和每步运行结果的话，读起来疑问会少很多，毕竟要让代码可执行得完全信息。

这里用二元线性回归来演示，最常见的就是用一元二次方程( $y=ax^2+bx+c$ )，也就是拟合曲线。既然是一元方程，为什么是二元回归？因为回归的二元是指有2个independent variable： $x, x^2$

依旧使用上面的x, y数据，首先让我们来生成X矩阵，包含 $x, x^2$ ，但要注意的是这里第一列加入了常量1，为了矩阵正定和求b（图中 ${\hat\beta}_0$ ）：

X = torch.stack([torch.ones(x.shape), x, x ** 2]).T

tensor([[ 1., 0., 0.],
[ 1., 1., 1.],
[ 1., 2., 4.],
[ 1., 3., 9.],
[ 1., 4., 16.],
[ 1., 5., 25.],
...
[ 1., 15., 225.],
[ 1., 16., 256.],
[ 1., 17., 289.],
[ 1., 18., 324.],
[ 1., 19., 361.]])

然后直接运算就行了：

b, m1, m2 = (X.T @ X).inverse() @ X.T @ y
print(b, m1, m2)

(tensor(220.5210), tensor(4.0694), tensor(-0.1735))

是的，这就是结果，让我们绘图看看：

plt.plot(x, y)
plt.plot(x, m1 * x + m2 * x**2 + b)
plt.show()

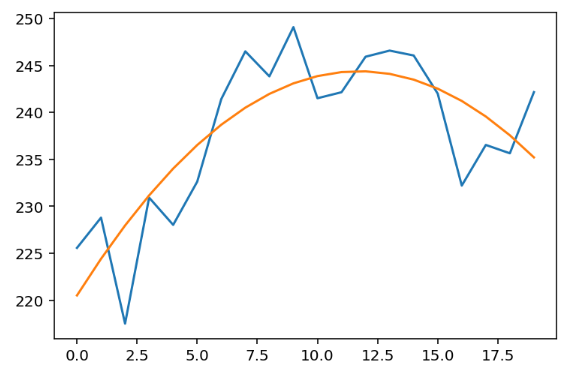
非常完美👏，是否很简单？但其实后面还有更重要的概念，比如多个解的情况和正交处理。

共线性和正交问题

实际使用中简单的进行多项式回归就能解决的问题并不常见，一般都是要对观察值进行回归，而观察值基本就不会完全独立，也就是x之间协方差不为0的。
保持x之间独立可以让coefficient只对该x负责不受其他x影响，这就需要正交调整。

具体不做细述，如果你想要快速解决问题，这里提供粗略的解决方案：使用qr decomposition。通过Q, R = torch.qr(X) 算出后，使用公式 $b, m_1,...,m_n=R^{-1}Q^Ty$ 来解决

有兴趣可以去看ESL 3.2.3 Multiple Regression from Simple Univariate Regression，用一元回归来多元回归。

作者：张戬昊 Heerozh (heerozh.com)

Heerozh's Blog